圖形結構
表示方法
基本上,在程式裡要表示圖的方式有分以下兩種。
相鄰矩陣 ( Adjacency Matrix )
所謂的相鄰矩陣就是根據項點數,建立一個N X N的矩陣,來表示圖形結構的方法,我們來看看下圖,你可以看到左邊為圖,右邊為矩陣,在矩陣中,每個1就代表該兩個項點有連線。
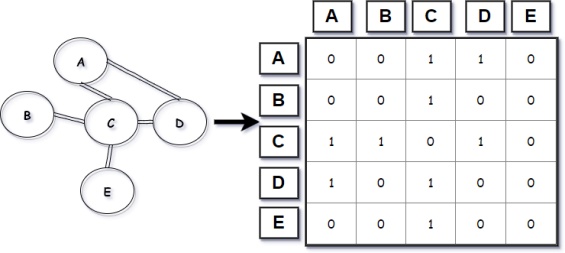
相鄰串列 ( Adjacency List )
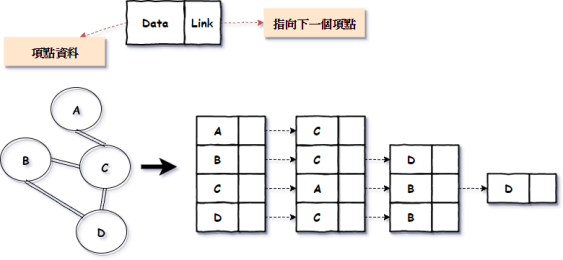
兩者的優缺點
基本上這兩者各有優缺點,我們列出下表來比較一下。

上面列表中有提到一個Complete Graph,它的定義如下。
假設有N個頂點,而每個頂點的邊數有N-1個,它就可以被稱為Complete Graph。
圖形結構的實作與方法操作方法實作
我們這邊的實作都以相鄰串列為主,我們主要會建立三個方法。
AddVertex : 新增頂點至graph中。
AddEdge : 新增邊來連結訂點。
Traveral : 該方法可以走訪graph中所有的頂點。
首先我們先建立graph所需要使用的物件,graph中會存放所有的頂點(vertex)與邊(edge)。
function Graph() {
this.vertexs = [];
this.edges = [];
}
接下來我們會建立兩個方法AddVertex與AddEdge,讓我們可以新增頂點與邊到graph中。
Graph.prototype.addVertex = function(vertex) {
this.vertexs.push(vertex);
this.edges[vertex] = [];
};
Graph.prototype.addEdge = function(vertexA, vertexB) {
this.edges[vertexA].push(vertexB);
this.edges[vertexB].push(vertexA);
};
最後我們建立一個print方法來看看我們建立出來的圖。
Graph.prototype.print = function() {
console.log(this.vertexs.map(function(vertex) {
return (vertex + " -> " + this.edges[vertex].join(" , ")).trim();
},this).join(" | "));
};
var graph = new Graph();
graph.addVertex("A");
graph.addVertex("B");
graph.addVertex("C");
graph.print();
graph.addEdge("A","B");
graph.addEdge("A","C");
graph.print();
我們在上述的程式碼中建立了三個頂點A、B、C,並且將A連結B和A連結C,所以我們簡單用腦袋想一下,畫出來的圖形應該是如下圖。
A
/ \
B C
來看看我們輸出的結果,雖然和上圖不一樣,但實際上是一樣的,A -> C,B代表這A這頂點連結這B與C。
A -> C , B | B -> A | C -> A
接下來我們要建立Traveral,這方法可以讓我們走訪所有的頂點,而且每個頂點只會走訪到一次 ; 傳統上有兩種走訪方式。
Depth First Search (DFS ; 深度優先搜尋)
這個方法主要是使用stack的概念來進行的,如果忘記stack的概念可至這篇文章複習複習。基礎資料結構(1)---陣列(Array)、堆疊(Stack)、佇列(Queue)
這個方法主要的過程如下。
把起點丟入stack中。
若stack不為空,則
從stack中,取出一個項點(它視為已走訪),並將此頂點所有相鄰且未走訪的頂點,丟到stack中。
若所有的頂點階已被走訪過,而stack仍不為空時,則將stack清空。
若stack為空,則完。
把以上過程說的更白文點就是
走訪起始頂點,然後尋找相鄰且未走訪的頂點,再做dfs,如果從任何已走訪過的頂點,都無法再走訪到一個尚未被走過的頂點時,則結束走訪。
以下就為實作的程式碼。
Graph.prototype.traverseDFS = function(startVertex, callback) {
if (!~this.vertexs.indexOf(startVertex)) {
return console.log("Vertex not found");
}
var visited = [];
_traverseDFS.call(this,startVertex,visited,callback);
function _traverseDFS(vertex, visited, callback) {
visited[vertex] = true;
if (this.edges[vertex] !== undefined) {
callback(vertex);
}
for (var i = 0; i < this.edges[vertex].length; i++) {
if (!visited[this.edges[vertex][i]]) {
_traverseDFS.call(this,this.edges[vertex][i], visited, callback);
}
}
}
};
而假設我們有如下的圖。
A
/ \
B C
/ \ /
D E F
然後我們看看執行DFS的結果。
A
C
F
B
D
E
看到了嗎這就是dfs的結果,如同它的名字深度,它會先針對單一個鄰近頂點就行深入的走訪,等到這條支線都走完,就開始走另外一條,Depth First Search這個方法也通時適用於我們前面說的樹狀結構的走訪。
Breadth First Search (BFS ; 廣度優先搜尋)
而BFS基本上運作流程與DFS差不多,只差在把stack改為queue,我們就直接看程式碼吧。
Graph.prototype.traverseBFS = function(startVertex,callback){
if (!~this.vertexs.indexOf(startVertex)) {
return console.log("Vertex not found");
}
var queue = [];
var visited = [];
queue.push(startVertex);
visited[startVertex] = true;
while(queue.length){
var vertex = queue.shift();
callback(vertex);
for (var i=0;i
if(!visited[this.edges[vertex][i]]){
visited[this.edges[vertex][i]] = true;
queue.push(this.edges[vertex][i]);
}
}
}
}
而假設我們有如下的圖。
A
/ \
B C
/ \ /
D E F
然後我們看看執行BFS的結果。
A
C
B
F
D
E
它就如同它的名稱Breadth First Search (BFS ; 廣度優先搜尋),它不是一條子線一直找下去,而是先廣泛的在四周先尋找,然後在尋找更後面一層的頂點。
Leetcode 判斷是否為樹
Example
Given n = 5 and edges = [[0, 1], [0, 2], [0, 3], [1, 4]], return true.
Given n = 5 and edges = [[0, 1], [1, 2], [2, 3], [1, 3], [1, 4]], return false.
public class Solution {
/*
* @param n: An integer
* @param edges: a list of undirected edges
* @return: true if it's a valid tree, or false
*/
public boolean validTree(int n, int[][] edges) {
// write your code here
if(n == 0){
return false;
}
if(edges.length != n - 1){
return false;
}
// Integer => 點
// Set => 點的所有鄰居
Map> graph = initializeGraph(n, edges);
// bfs
Queue queue = new LinkedList<>();
Set hash = new HashSet<>();
queue.offer(0);
hash.add(0);
while (queue.size() > 0){
int current = queue.poll();
for (Integer neighbor : graph.get(current)) {
if (hash.contains(neighbor)) {
continue;
}
hash.add(neighbor);
queue.offer(neighbor);
}
}
return (hash.size() == n);
}
private Map> initializeGraph(int n, int[][] edges){
Map> graph = new HashMap<>();
for (int i=0; i< n; i++){
graph.put(i, new HashSet());
}
for (int i=0; i< edges.length ; i++){
int u = edges[i][0];
int v = edges[i][1];
graph.get(u).add(v);
graph.get(v).add(u);
}
return graph;
}
}
visited[this.edges[vertex][i]] = true;
queue.push(this.edges[vertex][i]);
}
}
}
}
而假設我們有如下的圖。
A
/ \
B C
/ \ /
D E F
然後我們看看執行BFS的結果。
A
C
B
F
D
E
它就如同它的名稱Breadth First Search (BFS ; 廣度優先搜尋),它不是一條子線一直找下去,而是先廣泛的在四周先尋找,然後在尋找更後面一層的頂點。
Leetcode 判斷是否為樹
Example
Given n = 5 and edges = [[0, 1], [0, 2], [0, 3], [1, 4]], return true.
Given n = 5 and edges = [[0, 1], [1, 2], [2, 3], [1, 3], [1, 4]], return false.
public class Solution {
/*
* @param n: An integer
* @param edges: a list of undirected edges
* @return: true if it's a valid tree, or false
*/
public boolean validTree(int n, int[][] edges) {
// write your code here
if(n == 0){
return false;
}
if(edges.length != n - 1){
return false;
}
// Integer => 點
// Set
Map
// bfs
Queue
Set
queue.offer(0);
hash.add(0);
while (queue.size() > 0){
int current = queue.poll();
for (Integer neighbor : graph.get(current)) {
if (hash.contains(neighbor)) {
continue;
}
hash.add(neighbor);
queue.offer(neighbor);
}
}
return (hash.size() == n);
}
private Map
Map
for (int i=0; i< n; i++){
graph.put(i, new HashSet
}
for (int i=0; i< edges.length ; i++){
int u = edges[i][0];
int v = edges[i][1];
graph.get(u).add(v);
graph.get(v).add(u);
}
return graph;
}
}





