樹狀結構

實作二元樹

二元樹的定義 二元樹須符合樹狀結構的定義，且二元樹中每個節點的最大分支度(degree)為2，左邊的分支樹稱作left subtree(左子樹)，右邊的分支樹稱作right subtree(右子樹)。

使用陣列建立二元樹
可以使用陣列建立二元樹，如下二元樹範例，本範例二元樹有6個節點。



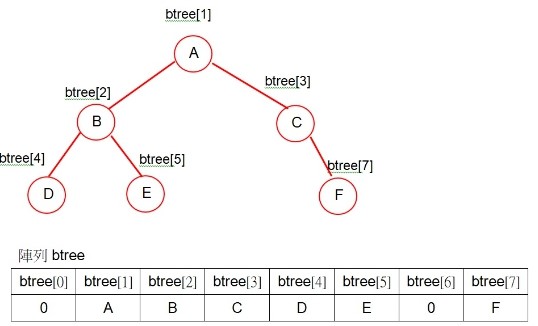
假設以陣列btree進行儲存，每個節點就依照點所在位置依序放入陣列中，若二元樹有空節點也必須保留該元素的陣列空間，並將0填入到該保留空間，在後面章節中「樹的走訪」單元會使用到這個保留空間，表示該節點沒有元素。點A為root(根節點)放置於陣列btree的索引值為1的元素內，點B為點A的左邊小孩，放置在陣列btree的索引值為2*(1)的元素內，點C為點A的右邊小孩，放置在陣列btree的索引值為2*(1)+1的元素內。點D為點B的左邊小孩，所以放置在陣列btree的索引值為2*(2)的元素內，點E為點B的右邊小孩，所以放置在陣列btree的索引值為2*(2)+1的元素內，依此類推。

可以獲得節點與索引值編號的規則如下，點X放置在陣列btree的索引值為n的元素內，點Y為點X的左邊小孩，就放置在陣列btree的索引值為2*(n)的元素內，點Z為點X的右邊小孩，就放置在陣列btree的索引值為2*(n)+1的元素內，有了此規則性才能使用程式存取二元樹的節點。 如果要使用陣列建立二元樹，程式碼如下。
#include
using namespace std;
char btree[1024];
int main(void){
memset(btree,0,sizeof(btree));
btree[1]='A';
btree[2]='B';
btree[3]='C';
btree[4]='D';
btree[5]='E';
btree[7]='F';
}