(一)資料結構學什麼

探討計算機系統所儲存(store)以及處理(process)的資料，並且學習如何組織這些資料，以及處理這些資料的方法。

(二)演算法定義

在有限步驟內解決數學問題的程序。 在計算機科學的領域中，演算法泛指"適合被實作為計算機程式的解題方法"

(三)程式的分析

(1)正確達到目的

(2)可維護性高

1.符合模組化原則，由上而下(top-down)的理解思路

2.常數、變數及函式(function)名稱是否有意義

3.函式的輸入、輸出及功能是否明確地定義

4.適當的地方加上註解

5.說明文件使否詳實完備

(3)效率高

(4)記憶體需求低

(四)Big-O符號

看出程式執行時間相對於問題大小的成長速度或成長趨勢

稱為程式或演算法的時間複雜度(time complexity)

常見的時間複雜度等級：

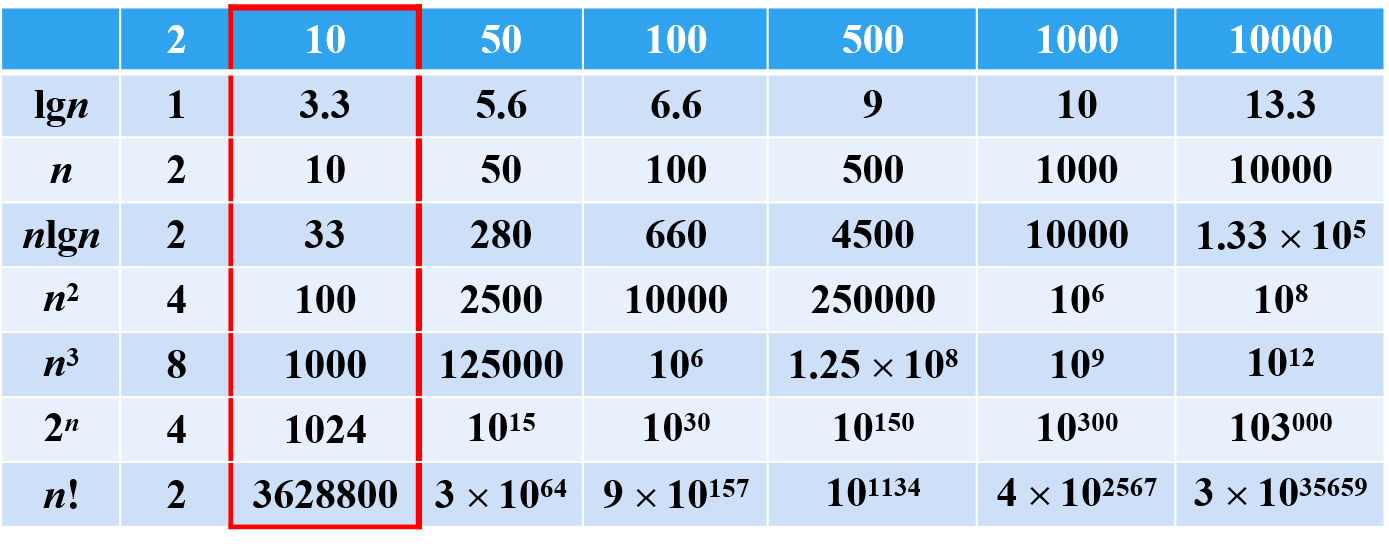
O(1)：常數級 (constant)

O(lgn)：對數級 (logarithmic)

O(n)：線性級 (linear)

O(nlgn)：對數-線性級 (log linear)

O(n2)：平方級 (quadratic)

O(n3)：立方級 (cubic)

O(2n)：指數級 (exponential)

O(n!)：階乘級 (factorial)

大小:O(1) < O(lgn) < O(n) < O(nlgn) < O(n2) < O(n3) < O(2n) < O(n!)